ChemSketchのテンプレート機能の使い方（３：新しいテンプレートの作成）

ChemSketchのテンプレート機能の使い方（３：新しいテンプレートの作成）

自分独自のテンプレートを作るのは、ざっくりとは、次の流れになります。

1. まず、テンプレートに入れたい構造式をいっぱい入れたファイルを作る
2. そのファイルをテンプレートとして登録する。

では、手順を追ってみます。

1. まず、描画ツールで、次の３つの構造式を書きます。

   

   テンプレートとして使いたい構造式を書く

   
   
2. これに名前を付けて、「.sk2」形式で保存します。

   

   「.sk2」形式で保存する

   
   
3. 「Templates」メニューから、「Template Organizer…」を選択します。

   

   Template Organizerを開く

   
   
4. 右下の「New…」を選択します。
   Templateに、このテンプレートに付けたい名前を入れ、Documentで、先ほど保存した.sk2ファイルを指定します。
   設定したら、「OK」です。

   

   テンプレート名を入れ、作成したファイルを選択

   
   
5. 元の画面に戻ると次のようになってます。
   「OK」を押して、オーガナイザーを閉じます。

   

   オーガナイザーに登録された

   
   
6. さて、うまくできたか見てみましょう。
   「Templates」＞「Template Window」を選択します。

   

   
   
7. 画面左のテンプレートのリストに正しく追加されていますね。

   

   正しくリストに表示された

   
   
8. それをクリックすると、先ほど作成した.sk2ファイルの中身が表示されます。

   

   
   
9. レイアウトは正しくできるでしょうか？テンプレート内の構造式をクリックして、描画エリアにマウスを移動して、クリックすると正しく配置されました。

もとの.sk2ファイルに構造を追加すれば、自分用のテンプレートがどんどん充実するというわけです。

もちろん、不要になった構造式が出てきたら、それを消すだけ。

ちなみに設定した.sk2ファイルを消したり、異動して指定していたパスからアクセスできないようにしたときはどうなるでしょうか？

Template Windowのリストから単純に消えてしまうだけです。「Template Window」というメニューを選択した時に、登録していたファイルがあるかどうかを判断して、なければリストに表示しないという仕組みのようです。

「テンプレートが見つかりません！」みたいなエラーは出ない感じです。

今日はここまで。

ChemSketchのテンプレート機能の使い方（２：その他の「Templates」メニュー項目）

ChemSketchのテンプレート機能の使い方
（２：その他の「Templates」メニュー項目）

前回に続いてChemSketchのテンプレート機能の続きです。

今回は「Table of Radicals」と「Periodic Table」について、本当に軽く。

ChemSketchの「Templates」メニュー

【Table of Radicals】

「Table of Radicals」を選ぶと、次の画面が表示されます。

「Table of Redicals」画面

ここで、左下にある「COOH」（Carboxyl：カルボキシル基）に、マウスポインタを重ねます。クリックすると、すぐに選択されてしまうので注意。

「Carboxyl」を選択

で、クリックします。

すると描画画面に、配置用のマウスポインターが表示されるので、大体の位置でクリックします。

配置されたら、あとは通常通りに続きを書いていけばOK。

例えば、画面右のボタンでシクロヘキサンを選んで、中央の炭素の上にマウスポインターを合わせると、次のように接続されたイメージが表示されます。

クリックすると確定。

「Table of Radicals」は右のメニューのボタンからも開くことができます。

【Periodic Table】

次は「Periodic Table」（周期表）です。

「Periodic Table」を選ぶと、次の画面が表示されます。

「Periodic Table」画面

動きとしては次のようになります。

ナトリウム（Na）を選択します。すると、ナトリウムに関する情報が表示されます。

Naを選択したところ

で、「OK」をクリックすると、描画画面に戻り、配置用のマウスカーソルになるので、適当な位置でクリックすると、ナトリウムイオン（Na+）が配置されます。

で、左のバーで「O」（酸素）を選び、Na+の少し右でクリックして配置します。

で、この2つを線でつなぎます。

ここで、「Table of Radicals」から、さっき使ったCarboxylを選んで、

「Table of Radicals」でCarboxylを選択

マウスポインターをH（水素）の上に持ってくると、結合イメージが表示されるので、クリックして確定すると、炭酸水素ナトリウムになります。

もう物質はぱっと見でわかるのですが、手順の復習のために、この構造式をPubChemでみてみます。

「Add-Ons」メニューから「Search PubChem」を選択します。

PubChemの検索メニュー

検索が終わると、次のような結果が返ってきます。

はい、正しく「炭酸水素ナトリウム」ですね。

PubChemの検索結果

今回は簡単すぎて、かつ、短いですけど。。。

ChemSketchのテンプレート機能の使い方（１：既存テンプレート）

ChemSketchのテンプレート機能の使い方
（１：既存テンプレート）

前回更新から、ずいぶんと期間が開いてしまいました。リアルが忙しい。

ChemSketchには便利なテンプレート機能があります。

予め登録されているものを使うこともできますが、自分で作成したものを登録することもできます。

書く時間を短縮する時には使ったほうがいいと思います。特に、今自分が関係している、あるいはよく使っている化合物などを登録しておけば、何度もゼロから書く必要がなくなります。

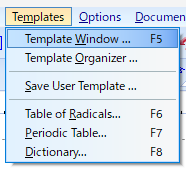
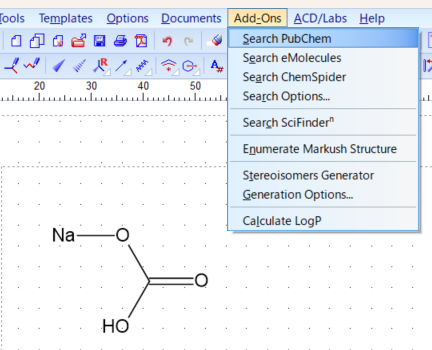
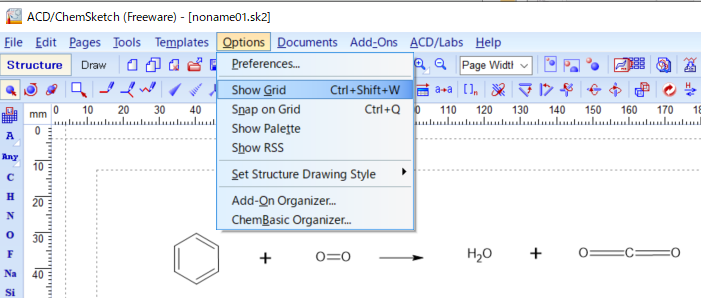
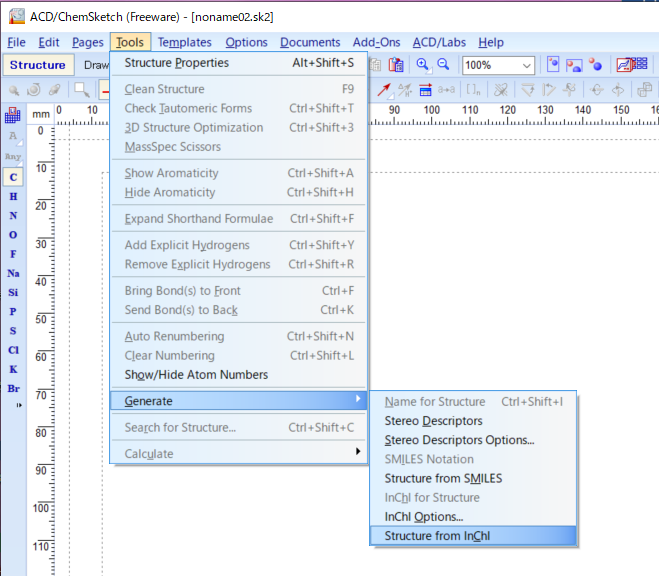
テンプレート関連の機能は「Templates」メニューに集約されています。

ChemSketchの「Templates」メニュー

【Template Window】

「Template Window…」を選ぶと、次のような大きな画面が開きます。

テンプレートのメイン画面

ただ、「Graphical Labels」「Lab Animals」「Lab Kit」「Virus and Vaccines」は、構造式ではないので、そんなに使うことはないかもしれないです。ただ、プレゼンの作成などの時には少しは使うかもしれないですが、初めから入っている図は頻度は低そうかも。後で書きますが、自分で使う画像を登録して活用することになるかと。

「Virus and Vaccines」テンプレートの内容

しかし、テンプレートはここだけでなく、画面上部のプルダウンメニューでさらに見ることができます。

もう一つのテンプレート選択メニュー

例えば、左でAromatics（芳香族）選ぶと、下のように２４種類が表示されます。

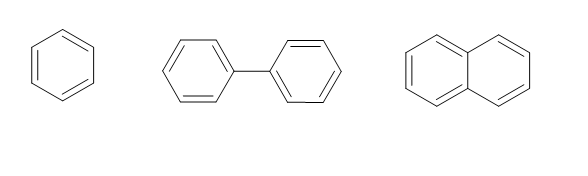
「Aromatics」テンプレートの内容

これに加えて、上のプルダウンメニューを見ると「1(5)」と書いています。これは５ページのうちの１ページ目ということを指しています。他のものも同じです。

ここで、「4(5) Cyclacenes&Phenacenes」（シクラセン＆フェナセン）を選ぶと、次のテンプレートが表示されます。

「4(5) Cyclacenes&Phenacenes」テンプレートの内容

もし、よく使うものがあれば、その位置を覚えてけばいいことになります。

＜テンプレートで選んだものを描画エリアに貼り付ける＞

テンプレートで目的のものを見つけたら、その構造にマウスを移動すると、四角い枠で囲まれます。

「１回」クリックすると、描画の画面に戻り、選んだ構造式の位置を決める表示になります。

ここで、うかつにクリックしてしまうと、場所が決まってしまうので、その時は後で移動する子になります。クリックは少し待って、位置を決めてから「１回」クリックするとそこに貼り付けられます。

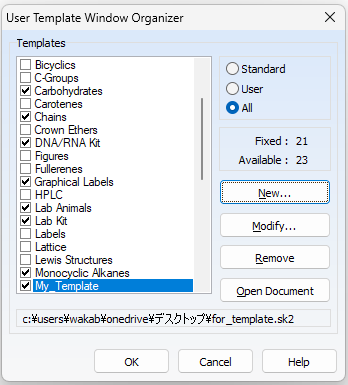
【Template Organizer】

「Template Organizer…」を選ぶと、次のような大きな画面が開きます。

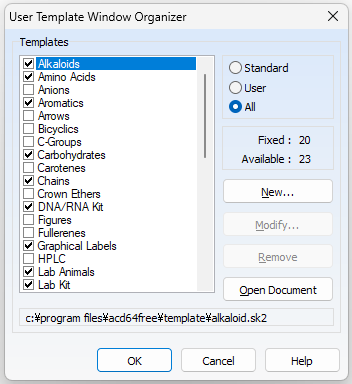
「Template Organizer」の画面

先ほど、テンプレートの左にメニューが２４種類ある、と書きましたが、実はここで表示する項目を選択できるのです。

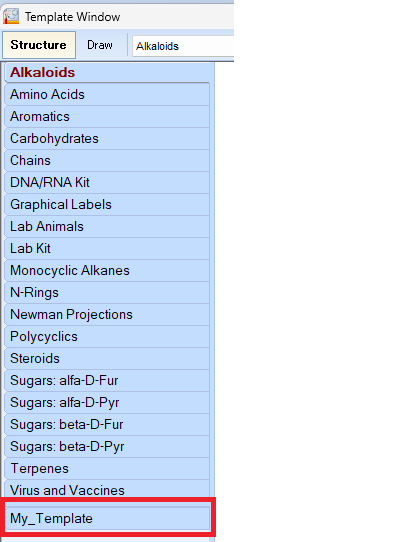
例えば、ここで「Bicycles」にチェックを入れて「OK」すると、

下のように、左のメニューに追加されます。

使うものを表示して、使わないものを非表示にしておけば、より効率的に使えます。

「Bicycles」テンプレートの内容

先ほどのOrganizerの画面で、「Open Document」ボタンをクリックすると少し面白いことが起きます。

リストから「Aromatics」を選んで、「Open Document」を選びます。

すると、次のアラートが表示されます。これは、デフォルトテンプレートは書き込みができず、読み取り専用なので編集できませんよ、という意味。

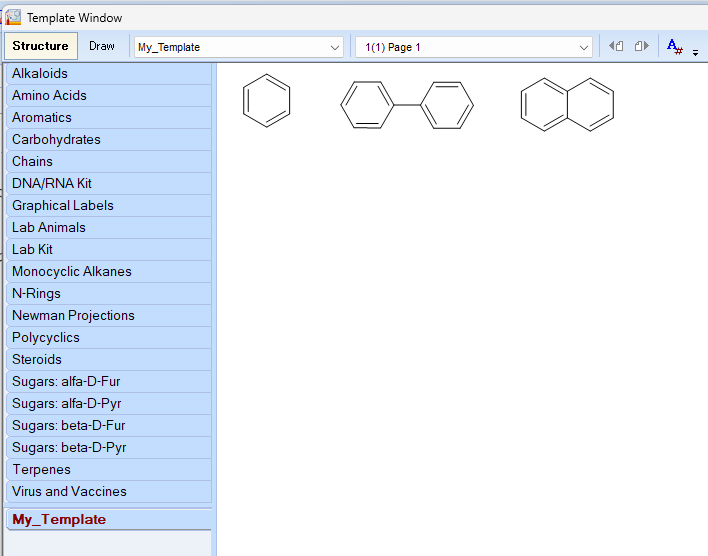
それでも開くと、描画画面に次のように表示されます。

テンプレート開いたところ

これは何でしょうか？

でよく見ると、さっきの画面の下に、ファイルのパス名が次にように書かれていて、それを開いているようです。

c:\program files\acd64free\template\aromatic.sk2

（ファイルを指している理由は独自のテンプレート追加するときに判明します）

では自由にこのパスを変更できるかといえば、固定になっている感じで、「他の芳香族はどこに行った？」と一瞬思います。

実は、画面に表示されているのはaromatic.sk2ファイルの「最終のページ」なのです。ChemSketchでは、１つのファイルに複数のページを持つことができるので、このボタンでファイルを開くときには、最終のページが開くようになっています。

「じゃあ、他のページは？」というと、画面の一番下にページ移動用のプルダウンメニューがあります。

ページ選択のメニュー

つまり、テンプレートというのは、ChemSketchで作成した普通の「.sk2」というファイルを登録している、ということがわかります。

ではでは。

ChemSketchでレイアウトを調整する

ChemSketchでレイアウトを調整する

少しご無沙汰でした。。。

以前に反応式を書いたときのように、それぞれの項目の微妙な調整をするときには少し設定を触っておいたほうが良いようです。

今回は

• ルーラーの表示
• グリッドの表示
• 印刷時のページの印刷範囲

の設定について書きます。

これらの設定はすべて「Options -> Preferences」でできます。

Option -> Preferences メニュー

これを選ぶと次の画面になります。

Preferences画面

ルーラーの表示

「View」のセクションの「Ruler」でオン／オフを切り替えます。デフォルトはオンです。

単位は「mm」になっています。これがどう設定されているかは、描画画面の左上のルーラーの原点あたりに「mm」と表示されていることでも確認できます。

単位は、「mm」「cm」「inch」「point」で指定できます。

ちなみに、「inch」に切り替えると、下のように表示されます。

インチ表示の場合

まあ、日本ではインチは使わないと思うので、デフォルトの「mm」でよいと思います。

「Guide」をオンにすると、マウスポインタの位置がルーラーに表示されます。

グリッドの表示

実際に書く時にはルーラーだけではうまく位置調整ができないので、グリッドを表示させます。

デフォルトでは表示されていないので、「Grid」のセクションの「Visible」をオンにします。次のようにグリッドが表示されます。

グリッドの表示

この設定で少し面白いところは、グリッドを直行だけではなく、６角形を書きやすくする「Vertically Hexagonal」「Herisontally Hexagonal」があることです。これを選ぶと、次のようになります。

Hexagonグリッドの表示

正直、グリッド表示するだけでは不足で、グリッドにスナップするようにしたほうが早いので、「Snap on Grid」をオンにします。

すると、各項目がグリッドのメモリに合わせて移動します。

印刷時のページの印刷範囲

用紙に印刷する場合、どこまで印刷されるかという範囲を示す点線が表示されています。

外側が「Printable Area」で、内側が「Page Margins」です。必要に応じて切り替えます。

ページのマージンはプリンタによって変わるので、印刷のときにうまくはまるように長さを設定しておく必要があります。その設定はこの画面にはありません。

「File->Page Setup」で長さを指定します。

「Page Setup」画面の「Margins」タブを選択すると、上下左右の印刷マージンを設定できます。

印刷マージンの設定

化学構造式をChemSketchから印刷するケースというのはあまり多くないでしょうね。多くの場合は、文章の間に埋め込むので、、、

簡単ですが、ここまで。

ChemSketchで化学反応式を書く

ChemSketchで化学反応式を書く

１つの分子を論文とかに貼るのであればわざわざソフトを使って構造式を書かなくても、オンラインのサービスなどから画像ファイルを取ってくるだけで済みます。

化学系の描画ソフトを使う必要が出てくるのは化学反応式を書くときでしょう。

ここでは、ChemSketchを使って、分子式で表された簡単な反応式を書く手順を書きます。

今回はベンゼンの燃焼。

C6H6 + O2 = CO2 + H2O

です。

1. ChemSketchの右のバーから「ベンゼン環」（Benzene）を選びます。

   

2. マウスカーソルで配置したい場所に行き、描画領域でぽちっとします。

   

   ここで、位置を動かしたいときは、左上の「Select/Move」を押して、今、配置したものを選択すれば動かせます。

   

3. 次は酸素。左側のツールバーで「O」（Oxygen）を選択して、描画領域でぽちっとします。すると、H2Oの水となります。なんか、イメージと違うなー。強制的に水素がつくんか。

   

4. この状態（つまり、まだ「O」が配置できる状態）で、表示されている水をぽちっとすると次のようになります。

   

5. で、ここで酸素間のボンドをプチっとすると、ようやく酸素になった。

   

   もっと簡単な手順があるのかな。
6. 上のツールバーから「＋」（Reaction Plus）を選択して、ベンゼンと酸素の間に置きます。

   

7. さて次は生成物側の水と二酸化炭素。水は、さっき出てきた「O」を使います。

   二酸化炭素は、次のようになります。CO2はそのままでもいいんですがあえて書き起こしてみます。

   意外と面倒？
8. 「C」をクリックして、まずはメタンを書きます。次に「O」クリックして水を２つ書きます。

   

9. で、これを線でつなぐと次のようになります。

   

10. 酸素のところでやったようにボンドをクリックして２重結合にすれば完成。

    

11. 見栄えを整理します。「Tools」メニューから「Clean Structure」を選びます。

    

12. で、最後に反応矢印です。

    

13. 段がついていたりするので、きれいに配置したいけど、反応式の「Clean」コマンドが見当たらない。。。

    仕方がないので今回はグリッドを表示して、手で成形した。

    まずはグリッドを表示。「Snap on Grid」をオンにしておけば、移動するときに、グリッドに従って移動できるので、比較的きれいにできます。

    

二酸化炭素を簡単に書く方法を探さなくては。。。

XMLファイルのテキスト部分だけを目立たせる方法（XMLBluePrint）

XMLファイルのテキスト部分だけを目立たせる方法（XMLBluePrint）

XMLファイルを編集するとき、不用意にタグを編集してしまうリスクを減らす必要があります。

もちろん、最終的にバリデーションするでしょうから、編集途中はあまり気にしなくてもよい、という人があるとは思いますが。。。

ただ、文章を編集する人が必ずしもXMLを良く知っているとは限らず、その人たちに「ここが触っていい部分だよ」と分かりやすくするほうが親切です。

タグをロックして触らせなないようするなど、高度な編集コントロールも考えられなくないですが、シンプルなXMLエディターで何かできないかと思いました。

最近、XMLエディターを「XMLBluePrint」に変えたんですが、その機能で、編集対象の文章部分だけ色を変える、ということしたので記録として書いておきます。

※    実は、私が使っているバージョンは執筆時点（2024/3/18）ではダウンロードできません。開発元に頼んで、これに関する問題を修正したバージョンを特別にもらいました。 なので、近い将来のバージョンで、ここに書いている機能は使えるようになると思います。

XMLBluePrintでXMLファイルを開くと次のようになっています。

タグには色がついているので、XMLがわかる人にはタグ部分とテキスト部分の区別はすぐにつくと思います。

また、「黒い文字の部分だけ編集してね」ということで済む場合もあります。

今回は、XMLBluePrintを使って。ここであえて編集可能な部分だけに色を付ける、という手順をまとめます。

「設定」＞「色…」を選択します。

「カテゴリ：」で「XML」を選択します。

「項目：」の欄から「Text」を選択します。

次に、「アイテムの背景色：」で、例えば「シアン」を選択します。

「OK」とすると、編集可能なテキスト部分だけ、シアンの背景色が表示されます。

例えば、編集途中で誤ってタグを編集すると下のように背景色がなくなるのですぐに「あっ、やばい」となるわけです（Ctrl+Zで戻します）。

ちなみに、行を折り返して表示する場合は、ツールバーのボタンを押すだけです。

表示はこんな感じになります。

今回の手順を踏んでも、本文中に「 」（空白文字）のような特殊文字を入れると色はつかないので注意が必要。

ではでは。

ChatGPT/GeminiでSMILES/InChIを生成させるとどうなるか

ChatGPT/GeminiでSMILES/InChIを生成させるとどうなるか

ではやってみます。

ChatGPT + SMILES

ChatGPTに「インドメタシンのSMILESを生成して」と入力します。

応答は、、、

念のため、ChemSketchで確認します。

1. ChatGPTの表記をコピーします。
2. ChemSketchの「Tools」＞「Generate」＞「Structure from SMILES」を選びます。

   

3. 画面に張り付けます。

   

4. 化学構造式が出ました。結果はこれ。

   

5. 違うな～。一応、PubChemにも飛んでみました。

   

ChatGPT + InChI

ChatGPTに「インドメタシンのInChI（ International Chemical Identifier）を生成して」と入力します。

応答は、、、

残念ながら、インドメタシンの具体的なInChI（International Chemical Identifier）を生成することはできません。InChIは、特定の分子構造を表現するための標準的な識別子であり、生成するには分子の具体的な構造情報が必要です。 インドメタシンの分子構造に基づいてInChIを生成するには、専門の化学情報ツールやデータベースを使用する必要があります。分子構造の描画や識別子生成には、ケモインフォマティクスツールやオンラインの分子構造データベースが利用されます。 化学情報システムや分子構造データベースのウェブサイトを利用して、インドメタシンのInChIを生成するか、既存のデータベースから取得することができます。

だめか。。。

Geminiではどうか。

Gemini + SMILES

Geminiに「インドメタシンのSMILESを生成して」と入力します。

応答は、、、

インドメタシンのSMILESは以下の通りです。 C1=CC(=O)C(=C1)C(=O)O SMILESは、化学物質の構造を表すための簡潔な表記法です。化学物質の原子と結合を、文字と数字の組み合わせで表します。 SMILESは、以下の用途に使用することができます。 ·        化学物質の構造の表示 ·        化学物質の検索 ·        化学物質の性質の予測 ·        化学物質の反応性の予測 参考資料 ·        SMILES: https://en.wikipedia.org/wiki/SMILES

さて取り込んでみます。

やはり違う。

Gemini + InChI

Geminiに「インドメタシンのInChI（ International Chemical Identifier）を生成して」と入力します。

応答は、、、

インドメタシンのInChIは、以下の2種類があります。 標準InChI: InChI=1S/C19H16ClNO2/c1-18(21)14-10-8-9-11-13(16(20)22)12-15-19-7-5-6-2-3-4/h5-6,8-9,11,13-15H,7H2,1-4H3/b14-10- InChIKey: InChIKey=QKZVKVKVKXDGJJ-UHFFFAOYSA-N 生成方法 これらのInChIは、以下の方法で生成しました。 1.      PubChemのウェブサイト (https://pubchem.ncbi.nlm.nih.gov/) にアクセスし、インドメタシンの検索を行います。 2.      検索結果から、インドメタシンの化合物ページを開きます。 3.      化合物ページの "Identifiers" セクションにある "InChI" または "InChIKey" のリンクをクリックします。 InChIの利用 InChIは、化学物質を識別するためのユニークなコードです。化学物質の構造、性質、反応性などを理解するために使用することができます。 InChIは、以下の用途に使用することができます。 ·        化学物質の検索 ·        化学物質の構造の比較 ·        化学物質の性質の予測 ·        化学物質の反応性の予測 参考資料 ·        PubChem: https://pubchem.ncbi.nlm.nih.gov/ ·        InChI: https://en.wikipedia.org/wiki/InChI

標準InChIのほうを使って、ChemSketchで構造式を書かせてみます。

「Tools」＞「Generate」＞「Structure from InChiI」を選択します。

貼り付けてもうまくいかない。

ちゃんとNIHのサイトにアクセスして取ってきてますが。

「そもそも生成AIに投入した日本語がうまく伝わっていないのでは？」と思い、英語にしてみました。

Generate SMILES for Indomethacin

おお、答えが違う。

Indomethacin actually has two types of SMILES: ·        Canonical SMILES: COc1ccc2c(c1)c(CC(=O)O)c(n2C(=O)c1ccc(cc1)Cl)C ·        Isomeric SMILES: (same as Canonical SMILES for Indomethacin) COc1ccc2c(c1)c(CC(=O)O)c(n2C(=O)c1ccc(cc1)Cl)C These can be found in resources like the IUPHAR/BPS Guide to Pharmacology (https://www.guidetopharmacology.org/).

Canonical SMILESでChemSketchに取り込んで、構造式を書かせると。

この構造をPubChemで検索しても正しいことが分かった。

【補足】

同じ英文をChatGPTに食わせると次の応答。

これをChemSketchで取り込むと。。。

残念。今回のテストはGeminiの勝ちかな。

生成AIの日本語の解釈は化学系の言葉ではうまくないことがわかります。

多分、絶対的な学習量が足りないんだろうな。